Advertisements
Advertisements
Question
ΔPQR is isosceles with PQ = QR. QR is extended to S so that ΔPRS becomes isosceles with PR = PS. Show that ∠PSRSP : ∠QPS = 1 : 3
Sum
Solution
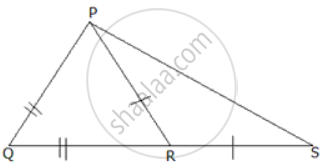
In ΔPQR,
PQ = QR ...(given)
∠PRQ = ∠QPR .....(i)
In ΔPRS,
PR = RS ...(given)
∠PSR = ∠RPS .......(ii)
Adding (i) and (ii)
∠QPR + ∠RPS = ∠PRQ + ∠PSR
∠QPS = ∠PRQ + ∠PSR .........(iii)
Now in PRS,
∠PRQ = ∠RPS + ∠PSR
∠PRQ = ∠PSR + ∠PSR ...(from (ii))
∠PRQ = 2∠PSR ..............(iv)
Now, ∠QPS = 2∠PSR + ∠PSR ...(from (iii) and (iv))
∠QPS = 3∠PSR
`(∠"PSR")/(∠"QPS") = (1)/(3)`
⇒ ∠PSR = ∠QPS = 1 : 3.
shaalaa.com
Is there an error in this question or solution?
