Advertisements
Advertisements
Question
पृथ्वी के पृष्ठ से ऊर्ध्वाधरतः ऊपर की ओर कोई रॉकेट 5 km s-1 की चाल से दागा जाता है। पृथ्वी पर वापस लौटने से पूर्व यह रॉकेट पृथ्वी से कितनी दूरी तक जाएगा? पृथ्वी का द्रव्यमान = 6.0 × 1024 kg; पृथ्वी की माध्य त्रिज्या = 6.4 × 106 m तथा G = 6.67 × 10-11N-m2/kg-2।
Solution
माना रॉकेट का द्रव्यमान = m; पृथ्वी से ऊर्ध्वाधरत: ऊपर की ओर रॉकेट का प्रक्षेप्य वेग ν = 5 किमी-से-1 = 5 × 10³ मी-से-1
माना रॉकेट पृथ्वी पर वापस लौटने से पूर्व पृथ्वी से अधिकतम दूरी H ऊँचाई तक जाता है। अत: इस ऊँचाई पर रॉकेट का वेग शून्य हो जाता है।
ऊर्जा संरक्षण सिद्धांत से पृथ्वी तल से महत्तम ऊँचाई पर पहुँचने पर रॉकेट की गतिज ऊर्जा में कमी = उसकी गुरुत्वीय स्थितिज ऊर्जा में वृद्धि -
`1/2 "mν"^2 - 0 = (- ("GM"_"e""m")/("R"_"e" + "H")) - (-( "GM"_"e""m")/"R"_"e")`
अथवा `1/2 "mν"^2 = "GM"_"e""m"[1/"R"_"e" - 1/("R"_"e" + "H")]`=`("GM"_"e""m"("R"_"e" + "H" - "R"_"e"))/("R"_"e"("R"_"e" + "H"))`
अथवा `1/2 "mν"^2 = ("GM"_"e""mH")/("R"_"e"^2 + "R"_"e""H")` अथवा `"ν"^2 = (2 "GM"_"e""H")/("R"_"e"^2 + "R"_"e""H")`
वज्रगुणन करके सरल करने पर, `"H" = ("R"_"e"^2 xx "ν"^2)/(2"GM"_"e" - "R"_"e""ν"^2)`
इस सूत्र में ज्ञात मान रखने पर,
`"H" = [((6.4 xx 10^6)^2(5 xx 10^3)^2)/(2 xx (6.67 xx 10^-11) xx (6.0 xx 10^24) - (6.4 xx 10^6)(5 xx 10^3)^2)]` m
= `1.6 xx 10^6` m
= `1600 xx 10^3` m
= 1600 km
APPEARS IN
RELATED QUESTIONS
यदि स्थितिज ऊर्जा का शून्य अनन्त पर है तो कक्षा में परिक्रमा करते किसी उपग्रह की कुल ऊर्जा इसकी ______ ऊर्जा का ऋणात्मक है।
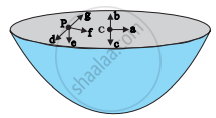
उपर्युक्त समस्या में किसी यादृच्छिक बिन्दु P पर गुरुत्वीय तीव्रता किस तीर द्वारा व्यक्त की जाएगी?
जैसा कि आपने इस अध्याय में सीखा है कि कोई तुल्यकाली उपग्रह पृथ्वी के पृष्ठ से लगभग 36,000 km ऊँचाई पर पृथ्वी की परिक्रमा करता है। इस उपग्रह के निर्धारित स्थल पर पृथ्वी के गुरुत्व बल के कारण विभव क्या है? (अनन्त पर स्थितिज ऊर्जा शून्य लीजिए) पृथ्वी का द्रव्यमान= 6.0 × 1024 kg, पृथ्वी की त्रिज्या= 6400 km.
कोई अन्तरिक्षयान मंगल पर ठहरा हुआ है। इस अन्तरिक्षयान पर कितनी ऊर्जा खर्च की जाए कि इसे सौरमण्डल से बाहर धकेला जा सके। अन्तरिक्षयान का द्रव्यमान = 1000 kg; सूर्य का द्रव्यमान = 2 × 1030 kg; मंगल का द्रव्यमान = 6.4 × 1023 kg; मंगल की त्रिज्या = 3395 km; मंगल की कक्षा की त्रिज्यां = 228 × 108 km तथा G = 6.67 × 10-11 N m2 kg-2.
किसी रॉकेट को मंगल के पृष्ठ से 2 kms-1 की चाल से ऊर्ध्वाधर ऊपर दागा जाता है। यदि मंगल के वातावरणीय प्रतिरोध के कारण इसकी 20% आरम्भिक ऊर्जा नष्ट हो जाती है, तब मंगल के पृष्ठ पर वापस लौटने से पूर्व यह रॉकेट मंगल से कितनी दूरी तक जाएगा? मंगल का द्रव्यमान = 6.4 × 1023 kg; मंगल की त्रिज्या = 3395 km तथा G = 6.67 × 10-11 N m2 kg-2.
