Question

Prove that in case of a prism, i + e = A + δ, where the symbols have their usual meanings.

Answer 1

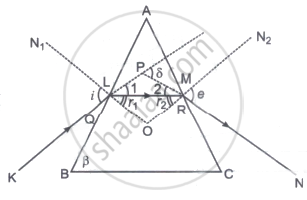
ΔABC is a principal section of the prism. A ray of light KL is incident on the face AB of the prism and the refracted ray LM is incident at r₂ on the face AC of the prism. The angle of deviation is δ.

In ΔPLM,  
δ = 1 + 2     ...(i)
i = 1 + r₁    ...(ii)
e = 2 + r₂   ...(iii)

On adding equation (ii) and (iii), we get

or i + e = 1 + 2 + r₁ + r₂

i + e = δ + r₁ + r₂    ...[from eq. (i)]   ...(iv)

Again  A + `angle"LOM" = angle 180^circ`   [opposite angles of a cyclic quadrilateral]  ...(v)

and r₁ + r₂ + ∠LOM = 180°     ...(vi)

From equations (v) and (vi),

A + ∠LOM = r₁ + r₂ + ∠LOM 

or A = r₁ + r₂     ...(vii)

Putting this value in (iv), we get

i + e = δ + A

which is the required relation.