Question

Prove that the line segments joining the mid points of the sides of a triangle form four triangles, each of which is similar to the original triangle

Answer 1

Given:* ∆ABC in which D, E, F are the mid-points of sides BC, CA and AB respectively.

To Prove: Each of the triangles AFE, FBD, EDC and DEF is similar to ∆ABC.

Proof: Consider triangles AFE and ABC.

Since F and E are mid-points of AB and AC respectively.

∴ FE || BC

⇒ ∠AEF = ∠B [Corresponding angles]

Thus, in ∆AFE and ∆ABC, we have

∠AFE = ∠B and, ∠A = ∠A [Common]

∴ ∆AFE ~ ∆ABC.

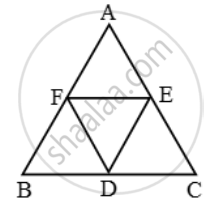
Similarly, we have

∆FBD ~ ∆ABC and ∆EDC ~ ∆ABC.

Now, we shall show that ∆DEF ~ ∆ABC.

Clearly, ED || AF and DE || EA.

∴ AFDE is a parallelogram.

⇒ ∠EDF = ∠A

[∵ Opposite angles of a parallelogram are equal]

Similarly, BDEF is a parallelogram.

∴ ∠DEF = ∠B

[∵ Opposite angles of a parallelogram are equal]

Thus, in triangles DEF and ABC, we have

∠EDF = ∠A and ∠DEF = ∠B

So, by AA-criterion of similarity, we have

∆DEF ~ ∆ABC.

Thus, each one of the triangles AFE, FBD, EDC and DEF is similar to ∆ABC.