Question

Prove that the points (a, b + c), (b, c + a) and (c, a + b) are collinear

Answer 1

Let ∆ be the area of the triangle formed by the points (a, b + c), (b, c + a) and (c, a + b).

We have,

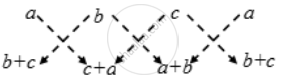
`∴ ∆ = \frac { 1 }{ 2 } |{a (c + a) + b (a + b) + c (b + c)} – {b (b+ c) + c (c + a) + a (a + b)}|`

`⇒ ∆ = \frac { 1 }{ 2 } |(ac + a^2 + ab + b^2 + bc + c^2 ) – (b^2 + bc + c^2 + ca + a^2 + ab)|`

⇒ ∆ = 0

Hence, the given points are collinear