Advertisements
Advertisements
Question
Prove that, tangent segments drawn from an external point to the circle are congruent.
Solution
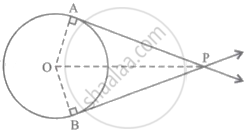
Point O is the centre of the circle and point P is external to the circle. Segment PA and segment PB are tangent segments to the circle. Point A and point B are touch points of the tangent segments.
Prove: PA ≅ PB
Construction: Draw OA, OB and OP.
Proof: Each tangent of a circle is perpendicular to the radius drawn through the point of contact ......(Theorem)
∴ Radius OA ⊥ AP and, Radius OB ⊥ BP .....(i)
∴ m∠PAO = 90° and m∠PBO = 90°
∴ ΔPAO and ΔPBO are right-angled triangles.
Now in ΔPAO and ΔPBO,
OA = OB ......(∵ Radius of same circle)
∴ ∠PAO = ∠PBO ......[Using (i)]
Hypotenuse OP = Hypotenuse OP ......(∵ Common side)
∴ ΔPAO ≅ ΔPBO .....(RHS congruency criterion)
∴ line PA ≅ line PB .....(∵ Corresponding sides of congruent triangles)
Line PA and line PB are tangent.
Hence proved.
