Advertisements
Advertisements
Question
Prove that the tangents at the extremities of any chord make equal angles with the chord.
Sum
Solution
Let AB be a chord of a circle with centre O, and let AP and BP be the tangents at A and B respectively.
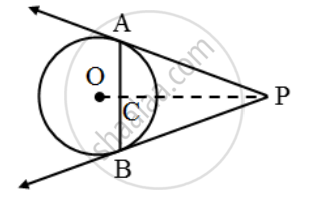
Suppose the tangents meet at P. Join OP. Suppose OP meets AB at C. We have to prove that ∠PAC = ∠PBC In triangles PCA and PCB, we have
PA = PB
[∵ Tangents from an external point are equal]
∠APC = ∠BPC
[∵PA and PB are equally inclined to OP] and, PC = PC [Common]
So, by SAS – criterion of congruence, we have
∆PAC ≅ ∆PBC
⇒ ∠PAC = ∠PBC
shaalaa.com
Is there an error in this question or solution?
