Advertisements
Advertisements
Question
रेख RM आणि रेख RN हे केंद्र O असलेल्या वर्तुळाचे स्पर्शिकाखंड आहेत, तर रेख OR हा ∠MRN आणि ∠MON या दोन्ही कोनांचा दुभाजक आहे, हे सिद्ध करा.
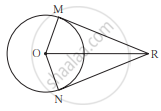
Solution
ΔOMR व ΔONR मध्ये,
रेख RM ≅ रेख RN ....[स्पर्शिकाखंडाचे प्रमेय]
रेख OM ≅ रेख ON ......[एकाच वर्तुळाच्या त्रिज्या]
रेख OR ≅ रेख OR ......[सामाईक बाजू]
∴ ΔOMR ≅ ΔONR ...[एकरूपतेची बाबाबा कसोटी]
∴ `{:(∠"MRO" ≅ ∠"NRO"), (∠"MOR" ≅ ∠"NOR"):}}` ....[एकरूप त्रिकोणांचे संगत कोन]
∴ रेख OR हा ∠MRN आणि ∠MON या दोन्ही कोनांचा दुभाजक आहे.
APPEARS IN
RELATED QUESTIONS
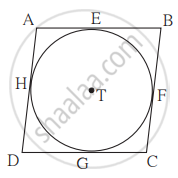
आकृती मध्ये, समांतरभुज `square`ABCD हा केंद्र T असलेल्या वर्तुळाभोवती परिलिखित केला आहे. (म्हणजे त्या चौकोनाच्या बाजू वर्तुळाला स्पर्श करतात.) बिंदू E, F, G आणि H हे स्पर्शबिंदू आहेत. जर AE = 4.5 आणि EB = 5.5, तर AD काढा.
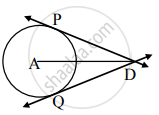
A केंद्र असलेल्या वर्तुळाला रेख DP आणि रेख DQ हे स्पर्शिकाखंड आहेत, जर DP = 7 सेमी, तर रेख DQ ची लांबी काढा?
आकृतीमध्ये, बिंदू O वर्तुळकेंद्र आणि रेख AB व रेख AC हे सपर्शिकाखंड आहेत. जर वर्तुळाची त्रिज्या r असेल आणि l(AB) = r असेल, तर `square`ABOC हा चौरस होतो हे दाखवण्यासाठी खालील कृती पूर्ण करा.
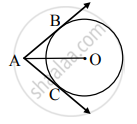
सिद्धता:
रेख OB आणि OC काढा.
l(AB) = r ..........…[पक्ष] (i)
AB = AC ..............`square` (ii)
परंतु, OB = OC = r .............`square` (iii)
∴ (i), (ii) व (iii) वरून
AB = `square` = OB = OC = r
∴ `square`ABOC हा `square` चौकोन आहे.
तसेच, ∠OBA = `square` .........[स्पर्शिका-त्रिज्या प्रमेय]
एक कोन काटकोन असणारा `square` चौकोन चौरस होतो.
∴ `square`ABOC हा चौरस आहे.
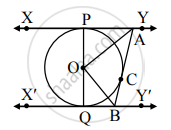
O केंद्र असलेल्या वर्तुळाचा रेख PQ हा व्यास आहे. बिंदू C मधून काढलेली स्पर्शिका वर्तुळास बिंदू P आणि Q बिंदूंतून काढलेल्या स्पर्शिकांना अनुक्रमे A आणि B बिंदूत छेदतात, तर सिद्ध करा, की ∠AOB = 90°
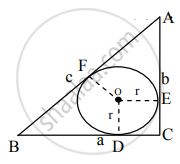
आकृतीमध्ये, ΔABC हा समद्विभुज त्रिकोण असून त्याची परिमिती 44 सेमी आहे. बाजू AB आणि बाजू BC एकरूप असून पाया AC ची लांबी 12 सेमी आहे. आकृतीत दाखवल्याप्रमाणे एक वर्तुळ तिन्ही बाजूंना स्पर्श करते, तर बिंदू B पासून वर्तुळास काढलेल्या स्पर्शिकाखंडाची लांबी काढा.
पक्ष: काटकोन ΔABC मध्ये एक वर्तुळ अंतर्लिखित केलेले आहे, ∠ACB = 90°. वर्तुळाची त्रिज्या r आहे.
साध्य: 2r = a + b – c
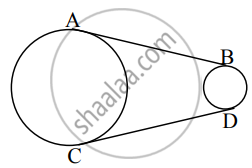
दोन असमान (भिन्न) त्रिज्यांच्या वर्तुळांमध्ये जर AB आणि CD त्यांच्या सामाईक स्पर्शिका असतील, तर रेख AB ≅ रेख CD दाखवा.
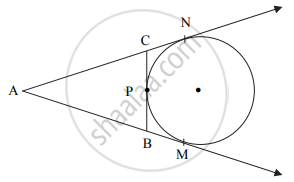
वरील आकृतिमध्ये दाखविल्याप्रमाणे, ΔABC च्या बाजू BC वरील P बिंदूत एक वर्तुळ बाहेरून स्पर्श करते. वाढवलेल्या रेषा AC व रेषा AB, त्या वर्तुळाला अनुक्रमे बिंदू N व बिंदू M मध्ये स्पर्श करतात. तर सिद्ध करा: AM = `1/2`(ΔABC ची परिमिती)
बिंदू O केंद्र घेऊन 3 सेमी त्रिज्येचे वर्तुळ काढा. या वर्तुळास P या बाह्यबिंदूतून रेख PA व रेख PB हे स्पर्शिकाखंड असे काढा की ∠APB 70°.
