Advertisements
Advertisements
Question
Represent geometrically the following number on the number line:
`sqrt(2.3)`
Solution
Draw a line segment such that AB = 2.3 units.
Mark C at a distance of 1 unit from B.
Mark O is the mid-point of AC.
Draw a semicircle with centre O and radius OC.
Draw a line perpendicular to AC, passing through B and intersecting the semicircle at D.
Now, BD = `sqrt(2.3)`.
Draw an arc with centre B and radius BD, meeting AC produced at E.
Then BE = BD = `sqrt(2.3)` units.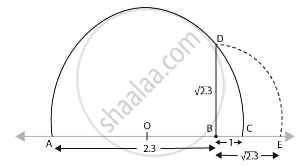
APPEARS IN
RELATED QUESTIONS
Represent `sqrt6,` `sqrt7,` `sqrt8` on the number line.
The number 0.318564318564318564 ........ is:
Every point on a number line represents
The number \[1 . \bar{{27}}\] in the form \[\frac{p}{q}\] , where p and q are integers and q ≠ 0, is
\[23 . \bar{{43}}\] when expressed in the form \[\frac{p}{q}\] (p, q are integers q ≠ 0), is
The smallest rational number by which`1/3`should be multiplied so that its decimal expansion terminates after one place of decimal, is
Represent the following numbers on the number line
`4.bar(73)` upto 4 decimal places
Represent the following number on the number line:
7.2
Locate `sqrt(5), sqrt(10)` and `sqrt(17)` on the number line.
Represent geometrically the following number on the number line:
`sqrt(4.5)`
