Question

Show graphically that each one of the following systems of equations has infinitely many solutions:

x − 2y + 11 = 0

3x − 6y + 33 = 0

Answer 1

The given equations are

x − 2y + 11 = 0   ...........(i)

3x − 6y + 33 = 0  .......(ii)

Putting x = 0 in equation (i) we get

`=> 0 - 2y = -11`

=> y = 11/2

x= 0, y = 11/2

Putting y = 0 in equation (i) we get

`=> x - 2x = -11`

=> x = -11

x= -11, y = 0

Use the following table to draw the graph.

x	0	-11
y	11/2	0

Draw the graph by plotting the two points A(0, 11/2), B(-11,0) from table.

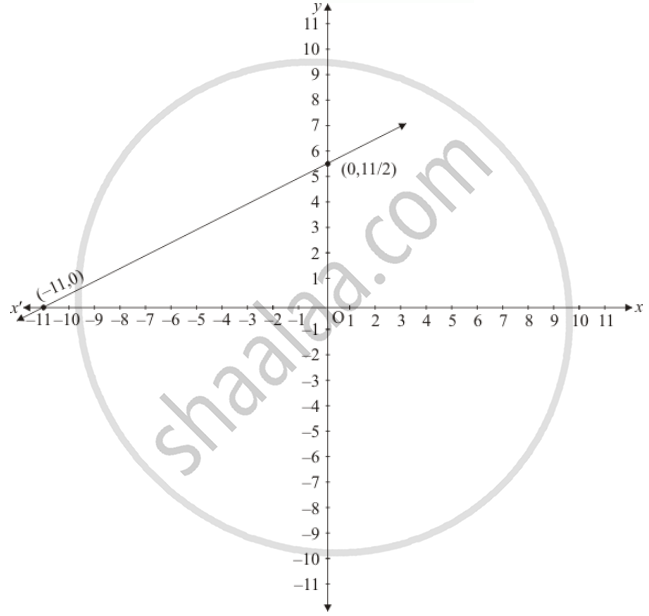
Graph of the equation .....(ii)

3x - 6y = -33   ....(ii)

Putting x = 0 in equation (ii) we get

`=> 3 xx 0 - 6y = -33`

`=> y = 11/2`

x = 0, y = 11/2

Putting y = 0 in equation (ii) we get

`=> 3x - 6 xx 0 = -33`

=> x = -11

x = -11, y = 0

Use the following table to draw the graph.

x	0	-11
y	11/2	0

Draw the graph by plotting the two points C(0, 11/2), D(-11,0) from table.

Thus the graph of the two equations are coincide

Consequently, every solution of one equation is a solution of the other.

Hence the equations have infinitely many solutions.