Question

Show that only odd harmonics are present in an air column vibrating in a pipe closed at one end.

Answer 1

Consider a narrow cylindrical pipe of length l that is closed at one end. When sound waves are sent down the air column in a cylindrical pipe that is closed at one end, they are reflected at the closed end with a phase reversal and at the open end without a phase reversal. Interference between incident and reflected waves creates stationary waves in the air column under the right conditions.

In this situation, stationary waves in the air column must satisfy two boundary conditions: a node at the closed end and an antinode at the open end. 

The resonating length of the air column is L = l + e, taking into account the end correction c at the open end.

The first mode of vibrations of air column closed at one end is as shown in Figure. 

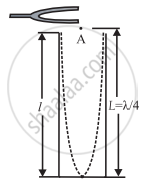
Let v be the speed of sound in air. This is the simplest mode of vibration of air column closed at one end and an antinode at the open end. The distance between a node and a subsequent antinode is equal to `λ/4`, where λ is the sound wavelength. The wavelength λ and frequency n are

∴ Length of air column: L = `λ/4` and λ = 4L

If n is the fundamental frequency, we have,

v = nλ

∴ n = `v/λ = v/(4L) = v/(4(l + e))`

The fundamental frequency is also known as the first harmonic.

In the second mode of vibration of the air column, two nodes and two antinodes are formed. If n₁ is the frequency and λ₁ is the wavelength of wave in this mode of vibrations in air column, we have,

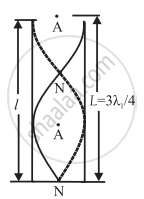
The length of the air column, L = `(3λ_1)/4`

The velocity in the second mode is given as v = n₁λ₁.

∴ n = `v/λ_1 = (3v)/(4L) = (3v)/(4(l + e))`

This frequency is called the third harmonics or first overtone. Similarly, during the third mode of vibration of the air column, three nodes and three antinodes are formed.

The next higher mode of vibrations of air column closed at one end is as shown in Figure.

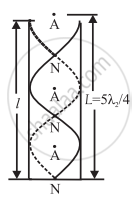
Here the same air column is made to vibrate in such a way that it contains a node at the closed end, an antinode at the open end with two more nodes and antinodes in between. If n₂ is the frequency and λ₂ is the wavelength of the wave in this mode of vibrations in air column, we have

The length of the air column, L = `(5λ_2)/4`

∴ λ₂ = `(4L)/5`

`n_2 = v/λ_2 ="5v"/(4L)=(5"v")/(4(l + e))=5"n"`

This frequency is called the fifth harmonic or second overtone.

Thus, we see that the frequencies of the modes of vibrations are in the ratio n: n₁: n₂ = 1: 3: 5. This shows that only odd harmonics are present in the modes of vibrations of the air column closed at one end.