Advertisements
Advertisements
Question
Show that only odd harmonics are present as overtones in the case of an air column vibrating in a pipe closed at one end.
Solution
The stationary waves in the air column, in this case, are subject to two boundary conditions that there must be a node at the closed end and an antinode at the open end. In what follows, we shall ignore the end correction.
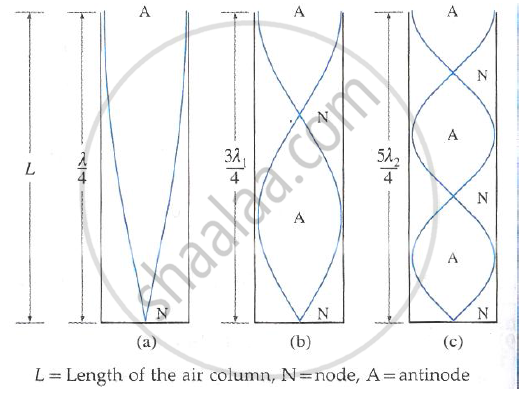
Let v be the speed of sound in air. In the simplest mode of vibration, as shown in the figure, there is a node at the closed end and an antinode at the open end. The distance between a node and a constructive antinode is `lambda/4`where `lambda` is the wavelength of sound. The corresponding wavelength `lambda` and frequency n are
`lambda = 4L " and " n = v/lambda = v/(4L)` ....(1)
This gives the fundamental frequency of vibration and the mode of vibration is called the fundamental mode or first harmonic.
In the next higher mode of vibration, the first overtune, two nodes and two antinodes are formed as shown in the figure. The corresponding wavelength `lambda_1` and frequency `lambda_1` are `lambda_2` are
`lambda_1 = (4L)/3` and `n_1 = v/lambda_1 = (3v)/(4L) = 3n` .....(2).
Therefore, the frequency in the first overtone is three times the fundamental frequency, i.e., the first overtone is the third hamonic.
In the second overtone, three nodes and three antinodes are formed as shown in the figure. The corresponding wavelength `lambda_2`and frequency `n_2` are `lambda_2 = (4L)/5` and `n_2 = v/lambda_2 = (5v)/(4L) = 5n` ...(3)
which is the fifth harmonic.
Therefore, in general, the frequency of the pth overtone (p = 1, 2, 3, ......) is
np = (2p + 1)n ......(4)
i.e., the pth overtone is the (2p + 1) the harmonic
Equations (1), (2) and (3) show that allowed frequencies in an air column are a pipe closed at one end and n, 3n, 5n, ...... That is, only odd harmonics are present as overtones.
APPEARS IN
RELATED QUESTIONS
The fundamental frequency of an air column in a pipe closed at one end is in unison with the third overtone of an open pipe. Calculate the ratio of lengths of their air columns
In a set, 21 turning forks are arranged in a series of decreasing frequencies. Each tuning fork produces 4 beats per second with the preceding fork. If the first fork is an octave of the last fork, find the frequencies of the first and tenth fork.
The value of end correction for an open organ pipe of radius 'r' is .........................
A) 0.3 r
B) 0.6 r
C) 0.9 r
D) 1.2 r
With a neat labelled diagram, show that all harmonics are present in an air column contained in a pipe open at both the ends. Define end correction.
A pipe which is open at both ends is 47 cm long and has an inner diameter 5 cm. If the speed of sound in air is 348 m/s, calculate the fundamental frequency of air column in that pipe.
A pipe open at both ends resonates to a frequency ‘n1’ and a pipe closed at one end resonates to a frequency ‘n2’. If they are joined to form a pipe closed at one end, then the fundamental frequency will be ______.
(A) `(n_1n_2)/(2n_2+n_1)`
(B) `(2n_2n_1)/(2n_2+n_1)`
(C) `(2n_2n_1)/(n_1+n_2)`
(D) `(n_2+2n_1)/(n_1n_2)`
Two sound notes have wavelengths 83/170 m and 83/172 m in the air. These notes when sounded together produce 8 beats per second. Calculate the velocity of sound in the air and frequencies of the two notes.
Discuss different modes of vibrations in an air column of a pipe open at both the ends.
State the cause of end correction.
Find the end correction for the pipe open at both the ends in fundamental mode.
A tube open at both ends has length 47 em. Calculate the fundamental frequency of air column. (Neglect end correction. Speed of sound in air is 3.3 x 102m/s}
Draw neat labelled diagrams for modes of vibration of an air column in a pipe when it is closed at one end.
Hence derive an expression for fundamental frequency in each case.
What is meant by harmonics?
Show that even as well as odd harmonics are present as overtones in the case of an air column vibrating in a pipe open at both the ends.
A wheel of moment of inertia 1 kg.m2 is rotating at a speed of 30 rad/s. Due to friction on the axis, it comes to rest in 10 minutes. Calculate the average torque of the friction.
In the law of tension, the fundamental frequency of the vibrating string is, ______
State law of tension.
State law of linear density.
What is the resonance?
How the frequency of the vibrating wire is affected if the load is fully immersed in water?
A sonometer wire of length 1 m is stretched by a weight of 10 kg. The fundamental frequency of vibration is 100 Hz. Determine the linear density of the material of the wire.
Waves produced by two vibrators in a medium have wavelength 2 m and 2.1 m respectively. When sounded together they produce 8 beats/second. Calculate wave velocity and frequencies of the vibrators.
State and verify the laws of vibrating strings using a sonometer.
Draw neat labelled diagrams for the first and second overtones of vibration of an air column in a pipe open at both ends.
