Advertisements
Advertisements
Question
Show that the function f : N → N defined by f(m) = m2 + m + 3 is one-one function
Solution
N = {1, 2, 3, 4, 5, …..}
f(m) = m2 + m + 3
f(1) = 12 + 1 + 3 = 5
f(2) = 22 + 2 + 3 = 9
f(3) = 32 + 3 + 3 = 15
f(4) = 42 + 4 + 3 = 23
f = {(1, 5) (2, 9) (3, 15) (4, 23)}
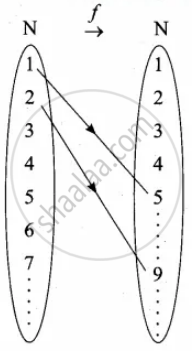
From the diagram we can understand different elements in (N) in the domain, there are different images in (N) co-domain.
∴ The function is a one-one function.
APPEARS IN
RELATED QUESTIONS
Show that the function f : N → N defined by f(x) = 2x – 1 is one-one but not onto
In the following case state whether the function is bijective or not. Justify your answer
f: R → R defined by f(x) = 2x + 1
In the following case state whether the function is bijective or not. Justify your answer
f: R → R defined by f(x) = 3 – 4x2
Let A = {–1, 1} and B = {0, 2}. If the function f: A → B defined by f(x) = ax + b is an onto function? Find a and b
The distance S object travel under the influence of gravity in time t seconds is given by S(t) = `1/2` gt2 + at + b where, (g is the acceleration due to gravity), a, b are constant. Verify whether the function S(t) is one-one or not.
Multiple choice question :
Let A = {1, 2, 3, 4} and B = {4, 8, 9, 10}. A function f: A → B given by f = {(1, 4), (2, 8), (3, 9), (4, 10)} is a
Multiple choice question :
If f : A → B is a bijective function and if n(B) = 7, then n(A) is equal to
Let A = {1, 2, 3, 4} and B = N. Let f : A → B be defined by f(x) = x3 then, identify the type of function
