Question

Show that the volume of the parallelopiped whose coterminus edges are `bara barb barc` is `[(bara, barb, barc)].`

Answer 1

Let `bar(OA), bar(OB)` and `bar(OC)` represent the coterminus edges `bara, barb` and `barc` respectively of the parallelopiped.

Draw seg AN perpendicular to the plane of `barb` and `barc`.

 
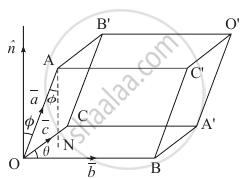
Let θ be the angle between `barb` and `barc` Φ be the angle between the line AN and `bara`.

∴ `(AN)/(OA)` = cos Φ

∴ AN = OA cos Φ = a cos Φ

If `hatn` is the unit vector perpendicular to the plane of `barb` and `barc`, then the angle between `bara` and `hatn` is also Φ.

Volume of the parallelopiped

= (area of parallelogram OBA'C) × AN

= (bc sin θ)(a cos Φ)

= a(bc sin θ) cos Φ    ...(1)

Now, let us consider the scalar triple product

`[(bara, barb, barc)] = bara*(barb xx barc)`

`barb xx barc = (bc sin θ)*hatn`

∴ `|barb xx barc|` = bc sin θ

∴ `[(bara, barb, barc)] = bara*(barb xx barc)`

= `|bara|*|barb xx barc| cos Φ`

= a(bc sin θ) cos Φ    ...(2)

From (1) and (2),

Volume of the parallelopiped = `[(bara, barb, barc)] `.