Question

Smaller area bounded by the circle `x^2 + y^2 = 4` and the line `x + y = 2` is.

Options

• `2(pi - 2)`

• `pi - 2`

• `2pi - 2`

• `2(pi + 2)`

Answer 1

`pi - 2`

Explanation:

A circle of radius 2 and centre at 0 is drawn. The line AB : `x + y` = 2 passes through (2, 0) and (0, 2).

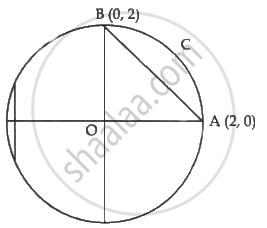
Area of the region ACB,

Area of quadrant OAB – Area of ΔOAB  ......(1)

Now, `x^2 + y^2` = 4

∴ `y^2 = 4 - x^2` or `y = sqrt(4 - x^2)`

∴ Area of quadrant OAB = `int_0^2 ydx = int_0^2 sqrt(4 - x^2)  dx`

=  `[x/2 sqrt(4 - x^2) + 4/2 sin^-1  x/2]_0^2`

`[because int sqrt(a^2 - x^2)  dx  x/2 sqrt(a^2 - x^2) + a^2/2 sin^-1  x/a]`

= `[0 + 2(sin^-1  2/2 - 0)]`

= `2 xx pi/2 = pi` sq.units

Area of ΔABC = Area of the region bounded by AB.

AB : `x + y` = 2 or `y = 2 - x`

And `x = 0, y = 0`

= `int_0^2 (2 - x) dx = [2x - x^2/2]_0^2 = (4 - 4/2) - (0)` = 2

Putting these values in (1)

Area of region ACB = `pi - 2`.