Question

समभुज चौकोनाच्या बाजूंच्या वर्गांची बेरीज त्याच्या कर्णाच्या वर्गांच्या बेरजेइतकी असते हे सिद्ध करण्यासाठी खालील कृती पूर्ण करा.

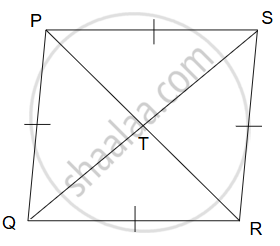
पक्ष: `square`PQRS हा समभुज चौकोन असून कर्ण PR आणि SQ एकमेकांना T या बिंदूत छेदतात.

साध्य: PS² + SR² + QR² + PQ² = PR² + QS²

कृती:

समभुज चौकोनाचे कर्ण परस्परांना दुभागतात.

ΔPQS मध्ये रेख PT ही मध्यगा आणि ΔQRS मध्ये रेख RT ही मध्यगा आहे.

∴ अपोलोनियसच्या प्रमेयानुसार

PQ² + PS² = `square` + 2QT²  ...(I)

QR² + SR² = `square` + 2QT²  ...(II)

(I) व (II) यांची बेरीज करू

PQ² + PS² + QR² + SR² = 2(PT² + `square`) + 4QT²

= 2(PT² + `square`) + 4QT²  ...(RT = PT)

= 4PT² + 4QT²

= (`square`)² + (2QT)²

∴ PQ² + PS² + QR² + SR² = PR² + `square`

Answer 1

पक्ष: `square`PQRS हा समभुज चौकोन असून कर्ण PR आणि SQ एकमेकांना T या बिंदूत छेदतात.

साध्य: PS² + SR² + QR² + PQ² = PR² + QS²

कृती:

समभुज चौकोनाचे कर्ण परस्परांना दुभागतात.

ΔPQS मध्ये रेख PT ही मध्यगा आणि ΔQRS मध्ये रेख RT ही मध्यगा आहे.

∴ अपोलोनियसच्या प्रमेयानुसार

PQ² + PS² = \[\boxed{2\text{PT}^2}\] + 2QT²  ...(I)

QR² + SR² = \[\boxed{2\text{RT}^2}\] + 2QT² ...(II)

(I) व (II) यांची बेरीज करू,

PQ² + PS² + QR² + SR² = \[{2(\text{PT}^2 + \boxed{\text{RT}^2})}\] + 4QT²

= \[{2(\text{PT}^2 + \boxed{\text{PT}^2})}\] + 4QT² ...(RT = PT)

= 4PT² + 4QT²

= \[\boxed{(2\text{PT)}^2}\] + (2QT)²

∴ PQ² + PS² + QR² + SR² = PR² + \[\boxed{\text{QS}^2}\]