Question

समद्विबाहु ΔABC में, ∠A, तथा ∠B के माप समान हैं। ∠ACD यह ∆ABC का एक बहिष्कोण है। ∠ACB तथा ∠ACD के माप क्रमशः (3x - 17)° तथा (8x + 10)°हो तो ∠ACB और ∠ACD के माप ज्ञात करें। ∠A और ∠B के माप भी ज्ञात करो।

Answer 1

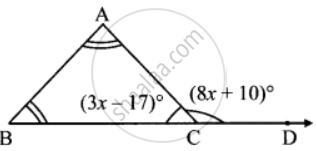
दिया गया:

∠ACB = (3x − 17)°

∠ACD = (8x + 10)°

अब, ∠ACB + ∠ACD = 180°                 ...(रेखीय युगल कोण)

⇒ 3x° − 17° + 8x + 10 = 180°

⇒ 3x° + 8x° − 17° + 10 = 180°

⇒ 11x° − 7° = 180°

⇒ 11x° – 7° + 7 = 180° + 7                 ...(दोनों तरफ 7 जोड़ने पर।)

⇒ 11x° = 187°

⇒ x° = `187°/11°`

⇒ x° = 17°

इसलिए,

∠ACB = (3x − 17)°

= (3 × 17)° − 17°

= (51 − 17)°

= 34°

​∠ACD = (8x + 10)°

= (8 × 17)° + 10°

= (136 + 10)°

= 146°

अब, ∠A + ∠B = ∠ACD                 ...(शीर्षाभिमुख कोण)

⇒ 2∠A = 146°    (∵ ∠A = ∠B)

⇒ ∠A = `146°/2`

⇒ ∠A = 73°

इसलिए, ∠ACB के माप, ∠ACD, ∠A और ∠B क्रमशः 146°, 34°, 73° और 73° हैं।