Question

Solve the following system of equations by cross-multiplication method ax + by = 1;  `bx + ay = \frac{(a+b)^{2}}{a^{2}+b^{2}-1`

Answer 1

The given system of equations can be written as

ax + by – 1 = 0 ….(1)

`bx+ay=\frac{(a+b)^{2}}{a^{2}+b^{2}}-1`

`\Rightarrowbx+ay=\frac{a^{2}+2ab+b^{2}-a^{2}-b^{2}}{a^{2}+b^{2}}`

`\Rightarrow bx+ay=\frac{2ab}{a^{2}+b^{2}}`

`\Rightarrow bx+ay-\frac{2ab}{a^{2}+b^{2}}=0 ….. (2)`

Rewritting the equations (1) and (2), we have

ax + by – 1 = 0

`\Rightarrow bx+ay-\frac{2ab}{a^{2}+b^{2}}=0`

Now, by cross-multiplication method, we have

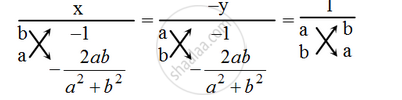
`\Rightarrow \frac{x}{b\times( \frac{-2ab}{a^{2}+b^{2}})-a\times (-1)}=\frac{-y}{a\times(\frac{-2ab}{a^{2}+b^{2}))-b\times (-1)}=\frac{1}{a\timesa-b\times b}`

`\Rightarrow\frac{x}{-\frac{2ab^{2}}{a^{2}+b^{2}}+a}=-y/((-2a^2b)/(a^2+b^2)+ b)=\frac{1}{a^{2}-b^2}`

`\Rightarrow\frac{x}{\frac{-2ab^{2}+a^{3}+ab^{2}}{a^{2}+b^{2}}}=-y/((-2a^2b+a^2b+b^3)/(a^2+b^2))=\frac{1}{a^{2}-b^{2}`

`=>x/((a(a^2-b^2))/(a^2+b^2))=(-y)/((b(b^2-a^2))/(a^2+b^2))=1/(a^2-b^2)`

`=>x/((a(a^2-b^2))/(a^2+b^2))=1/(a^2+b^2)=>x=a/(a^2+b^2)`

`"and "(-y)/((b(b^2-a^2))/(a^2+b^2))=1/(a^2+b^2)=>y=b/(a^2+b^2)`

Hence, the solution is ` x=\frac{a}{a^{2}+b^{2}},y=\frac{b}{a^{2}+b^{2}}`