Question

Solve the following system of equations by cross-multiplication method x + y = a – b; ax – by = a² + b²

Answer 1

The given system of equations can be rewritten as:
x + y – (a – b) = 0

ax – by – (a² + b² ) = 0

By cross-multiplication method, we have

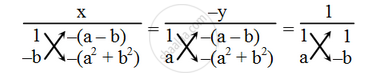
`\Rightarrow \frac{x}{-(a^{2}+b^{2})-(-b)\times\{-(a-b)\}}=\frac{-y}{-(a^{2}+b^{2})-a\times\{-(a-b)\}}=\frac{1}{-b-a}`

`\Rightarrow\frac{x}{-(a^{2}+b^{2})-b(a-b)}=\frac{-y}{-(a^{2}+b^{2})+a(a-b)}=\frac{1}{-(b+a)}`

`\Rightarrow\frac{x}{-a^{2}-b^{2}-ab+b^{2}}=\frac{-y}{-a^{2}-b^{2}+a^{2}-ab}=\frac{1}{-(a+b)}`

`\Rightarrow \frac{x}{-a(a+b)}=\frac{-y}{-b(a+b)}=\frac{1}{-(a+b)}`

`\Rightarrow \frac{x}{-a(a+b)}=\frac{1}{-(a+b)}\Rightarrow x=a`

`and\text{ }\frac{-y}{-b(a+b)}=\frac{1}{-(a+b)}\Rightarrow y=-b`