Question

Solve the following system of equations by the method of cross-multiplication.

11x + 15y = – 23; 7x – 2y = 20

Answer 1

The given system of equations is

11x + 15y + 23 = 0

7x – 2y – 20 = 0

Now, by cross-multiplication method, we have

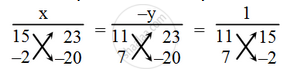
`\Rightarrow \frac{x}{15\times (-20)-(-2)\times 23}=\frac{-y}{11\times(-20)-7\times 23}=\frac{1}{11\times (-2)-7\times 15}`

`\Rightarrow \frac{x}{-300+46}=\frac{-y}{-220-161}=\frac{1}{-22-105}`

`​\Rightarrow \frac{x}{-254}=\frac{-y}{-381}=\frac{1}{-127}`

`​\Rightarrow \frac{x}{-254}=\frac{1}{-127}\Rightarrow x=2`

`\text{and}\frac{-y}{-381}=\frac{1}{-127}\Rightarrow \text{y}=-3`

Hence, x = 2, y = – 3 is the required solution.