Question

Solve the following system of equations by the method of cross-multiplication `\frac{x}{a}+\frac{y}{b}=a+b ;   \frac{x}{a^{2}}+\frac{y}{b^{2}}=2`

Answer 1

The given system of equations is rewritten as:

`\frac{x}{a}+\frac{y}{b}-( a+b) ….(1)`

`\frac{x}{a^{2}}+\frac{y}{b^{2}}-2 ….(2)`

Multiplying equation (1) by ab, we get

bx + ay – ab (a + b) = 0 ….(3)

Multiplying equation (2) by a^2 b^2 , we get

`b^2 x + a^2 y – 2a^2 b^2 = 0 ….(4)`

By cross multiplication method, we have

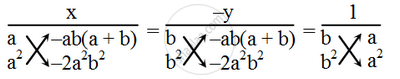
`\Rightarrow\frac{x}{-2a^{3}b^{2}+a^{3}b(a+b)}=\frac{-y}{-2a^{2}b^{3}+ab^{3}(a+b)}=\frac{1}{a^{2}b-ab^{2}`

`\Rightarrow\frac{x}{-2a^{3}b^{2}+a^{4}b+a^{3}b^{2}}=\frac{y}{-2a^{2}b^{3}+a^{2}b^{3}+ab^{4}}=\frac{1}{ab(a-b)}`

`\Rightarrow\frac{x}{a^{4}b-a^{3}b^{2}}=\frac{-y}{ab^{4}-a^{2}b^{3}}=\frac{1}{ab(a-b)}`

`\Rightarrow\frac{x}{a^{3}b(a-b)}=\frac{y}{ab^{3}(a-b)}=\frac{1}{ab(a-b)}`

`\Rightarrow \frac{x}{a^{3}b(a-b)}=\frac{1}{ab(a-b)}`

`\Rightarrow x=\frac{a^{3}b(a-b)}{ab(a-b)}=a^{2}`

`And\text{ }\frac{y}{ab^{3}(a-b)}=\frac{1}{ab(a-b)}`

`\Rightarrow y=\frac{ab^{3}(a-b)}{ab(a-b)}=b^{2}`

Hence, the solution x = a² , y = b²