Question

Solve the following system of equations in x and y by cross-multiplication method

`(a – b) x + (a + b) y = a^2 – 2ab – b^2`

`(a + b) (x + y) = a^2 + b^2`

Answer 1

The given system of equations can be rewritten as :

`(a – b) x + (a +b) y – (a^2 – 2ab – b^2 ) = 0`

`(a + b) x + (a + b) y – (a^2 + b^2 ) = 0`

By cross-multiplication method, we have

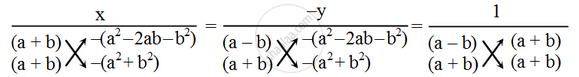
`\Rightarrow \frac{x}{(a+b)\times \{-(a^{2}+b^{2})\}-(a+b)\times\{-(a^{2}-2ab-b^{2})\}}=\frac{-y}{(a-b)\times\{-(a^{2}+b^{2})\}-(a+b)\times\{-(a^{2}-2ab-b^{2})\}}=\frac{1}{(a-b)\times (a+b)-(a+b)\times(a+b)}`

`\Rightarrow\frac{x}{-(a+b)(a^{2}+b^{2})+(a+b)(a^{2}-2ab-b^{2})}=\frac{-y}{-(a-b)(a^{2}+b^{2})+(a+b)(a^{2}-2ab-b^{2})}=\frac{1}{(a-b)(a+b)-(a+b)^{2}}`

`\Rightarrow\frac{x}{(a+b)[-(a^{2}+b^{2})+(a+b)(a^{2}-2ab-b^{2})]}=\frac{-y}{(a+b)(a^{2}-2ab-b^{2})-(a-b)(a^{2}+b^{2})}=\frac{1}{(a+b)(a-b-a-b)}`

`\Rightarrow\frac{x}{(a+b)(-2ab-2b^{2})}=\frac{-y}{a^{3}-a^{2}b-3ab^{2}-b^{3}-a^{3}-ab^{2}+a^{2}b+b^{3}}=\frac{1}{(a+b)(-2b)}`

`\Rightarrow\frac{x}{-(a+b)(2a+2b)b}=\frac{-y}{-4ab^{2}}=\frac{1}{-2b(a+b)}`

`\Rightarrow \frac{x}{-2(a+b)(a+b)b}=\frac{1}{-2b(a+b)}\Rightarrow x=a+b`

`and\text{ }\frac{-y}{-4ab^{2}}=\frac{1}{-2b(a+b)}\Rightarrowy=\frac{2ab}{a+b}`

Hence, the solution of the given system of equations is x = a + b,`y=\frac{2ab}{a+b}`