Question

Solve the following system of linear equations graphically
4x – 3y + 4 = 0, 4x + 3y – 20 = 0.
Find the area of the region bounded by these lines and the x-axis.

Answer 1

On a graph paper, draw a horizontal line X'OX and a vertical line YOY' as the x-axis and y-axis, respectively.
                               Graph of 4x - 3y + 4 = 0
4x - 3y + 4 = 0
⇒3y = (4x + 4)

∴ y = `(4x + 4)/3 `                   …(i)
Putting x = -1, we get y = 0.
Putting x = 2, we get y = 4.
Putting x = 5, we get y = 8.
Thus, we have the following table for the equation 4x - 3y + 4 = 0. 

x	-1	2	5
y	0	4	8

Now, plot the points A(-1, 0), B(2, 4) and C(5, 8) on the graph paper.
Join AB and BC to get the graph line AC. Extend it on both ways.
Thus, AC is the graph of 4x - 3y + 4 = 0.
                     Graph of 4x + 3y - 20 = 0
4x + 3y - 20 = 0
⇒ 3y = (–4x + 20)

∴ y `(-4x + 20 )/3`                         ……..(ii)
Putting x = 2, we get y = 4.
Putting x = -1, we get y = 8.
Putting x = 5, we get y = 0.
Thus, we have the following table for the equation 4x + 3y - 20 = 0.

x	2	-1	5
y	4	8	0

Now, plot the points P(1, -8) and Q(5, 0). The point B(2, 4) has already been plotted. Join PB and QB to get the graph line. Extend it on both ways.

Then, line PQ is the graph of the equation 4x + 3y - 20 = 0.

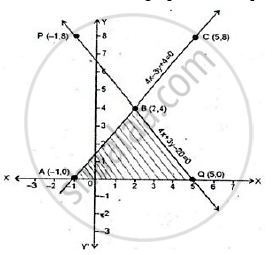
The two graph lines intersect at B(2, 4).
∴ The solution of the given system of equations is x = 2 and y = 4.
Clearly, the vertices of ΔABQ formed by these two lines and the x-axis are Q(5, 0), B(2, 4) and A(-1, 0).
Now, consider ΔABQ.
Here, height = 4 units and base (AQ) = 6 units
∴ Area ΔABQ =`1/2 xx base xx height sq . units `

                        =`1/2 xx 6 xx 4`

                        = 12 sq . units