Question

Solve the system of equations graphically:
2x + 3y + 5 = 0,
3x – 2y – 12 = 0

Answer 1

From the first equation, write y in terms of x

y = - `((5 + 2x)/3)`              …….(i)
Substitute different values of x in (i) to get different values of y

For x = -1, y = -`(5-2)/3 = -1`

For x = 2, y = - `(5+4)/3 = -3`

For x = 5, y = - `(5+4)/3 = -5`

Thus, the table for the first equation (2x + 3y + 5 = 0) is

x	-1	2	5
y	-1	-3	-5

Now, plot the points A (-1, -1), B (2, -3) and C (5, -5) on a graph paper and join them to get the graph of 2x + 3y + 5 = 0.
From the second equation, write y in terms of x

y =`(3x-12)/2`       …….(ii)
Now, substitute different values of x in (ii) to get different values of y
For x = 0, y =`(0-12)/2 = -6`

For x = 2, y = `(6-12)/2 = -3 `

For x = 4, y = `(12-12)/2 = 0`

So, the table for the second equation (3x – 2y – 12 = 0) is

x	0	2	4
y	-6	-3	0

Now, plot the points D (0, -6), E (2, -3) and F (4, 0) on the same graph paper and join D, E and F to get the graph of 3x – 2y – 12 = 0.

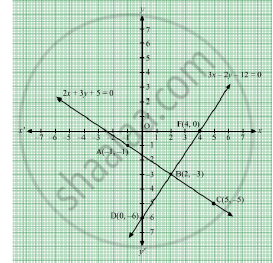
From the graph it is clear that, the given lines intersect at (2, -3).
Hence, the solution of the given system of equation is (2, -3).