Question

Solve the system of equations graphically:
2x - 5y + 4 = 0,
2x + y - 8 = 0

Answer 1

On a graph paper, draw a horizontal line X'OX and a vertical line YOY' as the x-axis and y-axis, respectively.

Graph of 2x - 5y + 4 = 0
2x – 5y + 4 = 0
⇒5y = (2x + 4)
⇒ `y=(2x+4)/5`    …(i)

Putting x = -2, we get y = 0.
Putting x = 3, we get y = 2.
Putting x = 8, we get y = 4.
Thus, we have the following table for the equation 2x - 5y + 4 = 0.

x	-2	3	8
y	0	2	4

Now, plot the points A (-2, 0), B (3, 2) and C(8, 4) on the graph paper.
Join AB and BC to get the graph line AC. Extend it on both ways.
Thus, AC is the graph of 2x - 5y + 4 = 0.

Graph of 2x + y - 8 = 0
2x + y - 8 = 0
⇒ y = (8 – 2x)      …(ii)
Putting x = 1, we get y = 6.
Putting x = 3, we get y = 2.
Putting x = 2, we get y = 4.
Thus, we have the following table for the equation 2x + y - 8 = 0.

x	1	3	2
y	6	2	4

Now, plot the points P (1, 6) and Q (2, 4). The point B (3, 2) has already been plotted. Join PQ and QB and extend it on both ways.
Thus, PB is the graph of 2x + y - 8 = 0.

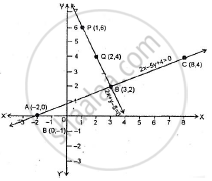
The two graph lines intersect at B (3, 2).
∴x = 3 and y = 2