Question

Solve the following :

Find the area of the ellipse `x^2/(25) + y^2/(16)` = 1 using integration

Answer 1

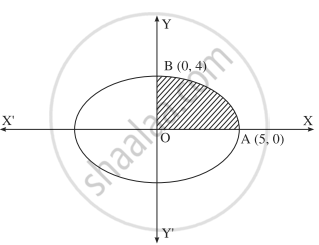
By the symmetry of the ellipse, its area is equal to 4 times the area of the region OABO. Clearly for this region, the limits of integration are 0 and 5.

From the equation of the ellipse

`y^2/(16) = 1 - x^2/(25) = (25 - x^2)/(25)`

∴ y² = `(16)/(25)(25 - x^2)`

In the first quadrant y > 0

∴ y = `(4)/(5)sqrt(25 - x^2)`

∴ Area of the ellipse = 4 (Area of the region OABO)

= `4int_0^5 y.dx`

= `4int_0^5 (4)/(5) sqrt(25 - x^2).dx`

= `(16)/(5) int_0^5 sqrt(25 - x^2).dx`

= `(16)/(5)[x/2 sqrt(25 - x^2) + (25)/(2)sin^-1 (x/5)]_0^5`

= `(16)/(5)(5/2 sqrt(25 - 25) + (25)/(2)sin^-1 (1)) - (16)/(5)[0/2 sqrt(25 - 0) + (25)/(2)sin^-1 (0)]`

= `(16)/(5) xx (25)/(2) xx pi/(2)`

= 20π sq. units.