Question

Solve the following LPP:

Maximize z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0.

Answer 1

First we draw the lines AB and CD whose equations are 3x + 5y = 26 and 5x + 3y = 30 respectively.

Line	Equation	Points on the X-axis	Points on the Y-axis	Sign	Region
AB	3x + 5y = 26	A`(26/3, 0)`	B `(0, 26/5)`	≤	origin side of line AB
CD	5x + 3y = 30	C(6, 0)	D(0, 10)	≤	origin side of line CD

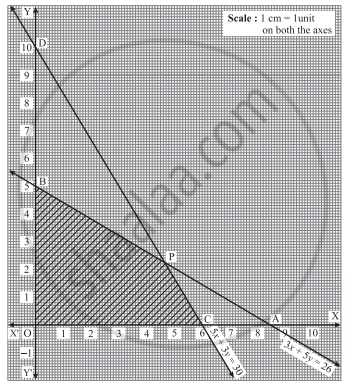
The feasible region is OCPBO which is shaded in the graph.

The vertices of the feasible region are O (0, 0), C (6, 0), P and B `(0, 26/5)`.

The vertex P is the point of intersection of the lines 3x + 5y = 26         .....(1)

and 5x + 3y = 30          .....(2)

Multiplying equation (1) by 3 and equation (2) by 5, we get

9x + 15y = 78

and 25x + 15y = 150

On subtracting, we get

16x = 72

∴ x = `72/16 = 9/2 = 4.5`

Substituting x = 4.5 in equation (2), we get

5(4.5) + 3y = 30

22.5 + 3y = 30

∴ 3y = 7.5

∴ y = 2.5

∴ P is (4.5, 2.5)

The values of the objective function z = 7x + 11y at these corner points are

z(O) = 7(0) + 11(0) = 0 + 0 = 0

z(C) = 7(6) + 11(0) = 42 + 0 = 42

z(P) = 7(4.5) + 11(2.5) = 31.5 + 27.5 = 59.0 = 59

z(B) = 7(0) + 11`(26/5) = 286/5 = 57.2`

∴ z has maximum value 59, when x = 4.5 and y = 2.5.