Question

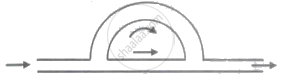
Sound waves are passing through two routes one in straight path and the other along a semicircular path of radius r and are again combined into one pipe and superposed as shown in the figure. If the velocity of sound waves in the pipe is v, then frequencies of resultant waves of maximum amplitude will be integral multiples of ______.

Options

• `v/(r(π - 2))`

• `v/(r(π - 1))`

• `(2v)/(r(π - 1))`

• `v/(r(π + 1))`

Answer 1

Sound waves are passing through two routes one in straight path and the other along a semicircular path of radius r and are again combined into one pipe and superposed as shown in the figure. If the velocity of sound waves in the pipe is v, then frequencies of resultant waves of maximum amplitude will be integral multiples of `(v)/(r(π-2)`.

Explanation:

Path difference= (πr - 2r) = (π - 2)r = mλ.. Where, m is the integral multiple (Say)

∴ `v=n xx λ ⇒ n= v/λ=[v/((πr - 2)r)] m`