Advertisements
Advertisements
Question
State Newton’s third law of motion and give two examples to illustrate the law.
Solution
According to Newton’s third law of motion, whenever one body exerts a force on another body, the second body exerts an equal and opposite force on the first body.
Examples:
(i) Jet airplanes utilize the principle of action and reaction. In the modern jet aircraft, the hot gases obtained by the rapid burning of fuel rush out of a jet from the rear end of the aircraft at a great speed. The equal and opposite reaction of the backward-heading gases pushes the aircraft forward at a great speed.
(ii) While rowing a boat, the boatman pushes the water backwards with the oars. The water exerts an equal and opposite push on the boat which makes the boat move forward. In fact, harder the boatman pushes back the water with the oars, greater is the reaction force exerted by water and faster moves the boat, in forward direction.
APPEARS IN
RELATED QUESTIONS
If action is always equal to the reaction, explain how a horse can pull a cart.
A girl weighing 25 kg stands on the tloor. She exerts a downward force of 250 N on the floor. What force does the floor exert on her ?
If action is always equal to reaction, explain why a cart pulled by a horse can be moved.
Explain how a rocket works.
Do action and reaction act on the same body or different bodies ? How are they related in magnitude and direction ? Are they simultaneous or not ?
Explain why, a runner presses the ground with his feet before he starts his run.
Name the law involved in the following situation :
when person A standing on roller skates pushes another person B (also standing on roller skates) and makes him move to the right side, then the person A himself gets moved to the left side by an equal distance.
Explain why, when a fireman directs a powerful stream of water on a fire from a hose pipe, the hose pipe tends to go backward.
According to the third law of motion, action and reaction :
Consider a frame that is made up of two thin massless rods AB and AC as shown in the figure. A vertical force `vec"P"` of magnitude 100 N is applied at point A of the frame.
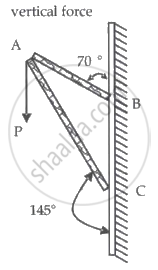
Suppose the force is `vec"P"` resolved parallel to the arms AB and AC of the frame.
The magnitude of the resolved component along the arm AC is xN.
The value of x, to the nearest integer, is ______.
[Given: sin(35°) = 0.573, cos(35°) = 0.819, sin(110°) = 0.939, cos(110°) = –0.342]
