Question

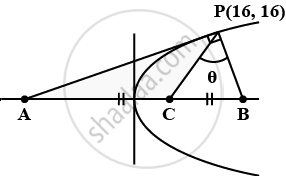
Tangent and normal are drawn at P(16, 16) on the parabola y² = 16x, which intersect the axis of the parabola at A and B, respectively. If C is the centre of the circle through the points P, A and B and ∠CPB = θ, then a value of tan θ is:

Options

• 2

• 3

• `4/3`

• `1/2`

Answer 1

2

Explanation:

PAB is a right-angled triangle with P as the right angle.

As a result, the circle circumscribing the right-angled triangle APB will have the hypotenuse (AB) as its diameter.

C will be the midpoint of AB because it is the centre of the circle.

Now given curve is y² = 16x

⇒ `2y  (dy)/(dx)` = 16

`|(dy)/(dx)|_((16"," 16)) = 8/16 = 1/2`

Equation of PA: `(y - 16) = 1/2 (x - 16)`

⇒ 2y – 32 = x – 16

⇒ `- x/16 + y/8` = 1

Equation of PB: (y – 16) = – 2(x – 16)

⇒ 2x + y = 48

⇒ `x/24 + y/28` = 1

So, A = (– 16, 0), B = (24, 0)

C = `((-16 + 24)/2, 0)` = (4, 0)

So, slope of CP is `(16 - 0)/(16 - 4) = 4/3`

We know, the slope of P B = – 2

m₁ = `4/3`, m₂ = – 2

tan θ = `|(m_1 - m_2)/(1 + m_1m_2)|`

= `|(4/3 + 2)/(1 - 8/3)|`

= `|(4 + 6)/(3 - 8)|` = 2

As a result, tan = 2