Question

The altitude through vertex C of a triangle ABC, with position vectors of vertices `veca, vecb, vecc` respectively is:

Options

• `(|vecb xx vecc + vecc xx veca + veca xx vecb|)/(|vecb - veca|)`

• `(|veca + vecb + vecc|)/(|vecb - veca|)`

• `(|vecb xx vecc + vecc xx veca + veca xx vecb|)/(|vecb xx veca|)`

• None of these

Answer 1

`(|vecb xx vecc + vecc xx veca + veca xx vecb|)/(|vecb - veca|)`

Explanation:

Let CM be the altitude through C.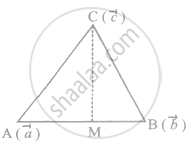

Then, area of triangle ABC

= `1/2 (AB)(CM) = 1/2 |vecb - veca| CM`  ......(i)

Again, area of triangle ABC

= `1/2 |vec(AB) xx vec(AC)|`

= `1/2 |(vecb - veca) xx (vecc - veca)|`

= `1/2|vecb xx vecc + vecc xx veca + veca xx vecb|`  ......(ii)

From (i) and (ii),

CM = `(|vecb xx vecc + vecc xx veca + veca xx vecb|)/(|vecb - veca|)`