Question

The angle between two adjacent sides `overlinea` and `overlineb` of parallelogram is `pi/6`. if `overlinea` = (2, -2, 1) and `|overlineb| = 2|overlinea|`, then area of this parallelogram is ______ 

Options

• 9

• 18

• `9/2`

• `3/4`

Answer 1

The angle between two adjacent sides `overlinea` and `overlineb` of parallelogram is `pi/6`. if `overlinea` = (2, -2, 1) and `|overlineb| = 2|overlinea|`, then area of this parallelogram is 9.

Explanation:

 

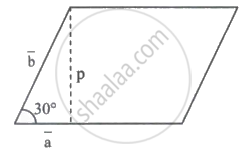
`overlinea = 2hati - 2hatj + hatk`

⇒ `|overlinea| = sqrt(4 + 4 + 1) = 3`

`|overlineb| = 2|overlinea| = 2(3) = 6`

sin 30° = `p/|overlineb|`

⇒ `1/2 = p/6 ⇒ p = 3`

∴ Area of parallelogram = 3 × 3 = 9