Question

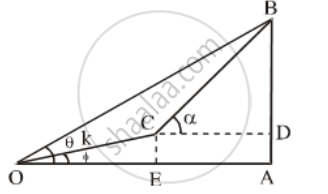
The angle of elevation of a cliff from a fixed point is θ. After going up a distance of k metres towards the top of cliff at an angle of φ, it is found that the angle of elevation is α. Show that the height of the cliff is metres

Answer 1

Let AB be the cliff and O be the fixed point such that the angle of elevation of the cliff from O is θ i.e. ∠AOB = θ. Let ∠AOC = φ and OC = k metres. From C draw CD and CE perpendiculars on AB and OA respectively.

Then, ∠DCB = α.

Let h be the height of the cliff AB.

In ∆OCE, we have

`\sin \phi =\frac{CE}{OC}`

`\Rightarrow \sin \phi =\frac{CE}{k}`

⇒ CE = k sin φ …(i) [∵ CE = AD]

⇒ AD = k sin φ

`\text{And, cos}\phi =\frac{OE}{OC}`

`\Rightarrow \text{cos}\phi =\frac{OE}{k}`

⇒ OE = k cos φ ….(ii)

In ∆ OAB, we have

`\text{tan }\theta =\frac{AB}{OA}`

`\Rightarrow \text{tan }\theta =\frac{h}{OA}`

⇒ OA = h cot θ ….(iii)

CD = EA = OA – OE

= h cot θ – k cos φ …..(iv) [Using eqs.(ii) and (iii)]

and, BD = AB – AD = AB – CE

= (h – k sin φ) ….(v) [Using equation (i)]

In ∆BCD, we have

`\text{tan}\alpha =\frac{BD}{CD}\Rightarrow \text{ tan}\alpha=\frac{h-k\sin \varphi }{h\cot \theta -k\cos \varphi }`

[Using equations (iv) and (v)]

`\Rightarrow \frac{1}{\cot \alpha }=\frac{h-k\sin \varphi }{h\cot \theta-k\cos \varphi}`

⇒ h cot α – k sin φ cot α = h cot θ – k cos φ

⇒ h(cot θ – cot α) = k(cos φ – sin φcot α)

`h= k((cos φ – sin φcot α))/((cot θ – cot α))`