Question

The angle of elevation of the top of a vertical tower from a point A, due east of it is 45°. The angle of elevation of the top of the same tower from a point B, due south of A is 30°. If the distance between A and B is `54sqrt(2)` m, then the height of the tower (in metres), is ______.

Options

• 108

• `36sqrt(3)`

• `54sqrt(3)`

• 54

Answer 1

The angle of elevation of the top of a vertical tower from a point A, due east of it is 45°. The angle of elevation of the top of the same tower from a point B, due south of A is 30°. If the distance between A and B is `54sqrt(2)` m, then the height of the tower (in metres), is 54.

Explanation:

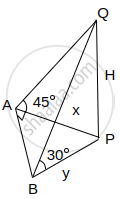
Let AP = x

BP = y

In rt. ΔAPQ

tan 45° = `H/x` `\implies` H = x

In rt. ΔBPQ

tan 30° = `H/y` `\implies` y = `sqrt(3)H`

In rt. ΔABP

`x^2 + (54sqrt(2))^2` = y²

`\implies H^2 + (54sqrt(2))^2` = 3H²

`\implies (54sqrt(2))^2` = 2H²

`\implies 54sqrt(2) = sqrt(2)H`

`\implies` 54 = H