Question

The angle of elevation of the top of a vertical tower from a point on the ground is 60°. From another point, 10 m vertically above the first, its angle of elevation is 45°. Find the height of the tower.

Options

• `5 (sqrt3 + 3)  "m"`

• `(sqrt3 + 3)  "m"`

• `15 (sqrt3 + 3)`

• `5 sqrt3`

Answer 1

`5 (sqrt3 + 3)  "m"`

Explanation:

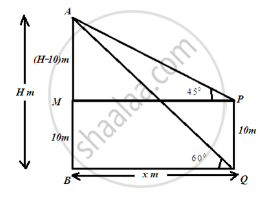
From figure,

`"tan"  60^circ = "AB"/"QB"`

`=> sqrt3 = "H"/"x"`

`=> "x" = "H"/sqrt3`

Also,

`"tan"  45^circ = ("H" - 10)/"x"`

`=> 1 = ("H" - 10)/"x"`

`=> "x" = "H" - 10`

Therefore,

`"H"/sqrt3 = "H" - 10`

`=> "H" - "H"/sqrt3 = 10`

`=> "H" = (10 sqrt3)/(sqrt3 - 1)`

`=> "H" = (10 sqrt3)/(sqrt3 - 1) xx (sqrt3 - 1)/(sqrt3 - 1)`

`=> "H" = 5 (sqrt3 + 3)  "m"`