Question

The angles of a triangle, two of whose sides are represented by the vectors `sqrt(3)(veca xx vecb)` and `vecb - (veca.vecb)veca` where `vecb` is a non-zero vector and `veca` is a unit vector are ______.

Options

• `tan^-1(1/sqrt(3)); tan^-1(1/2); tan^-1((sqrt(3) + 2)/(1 - 2sqrt(3)))`

• `tan^-1(sqrt(3)); tan^-1(1/sqrt(3)); cot^-1(0)`

• `tan^-1(sqrt(3)); tan^-1 (2) tan^-1((sqrt(3) + 2)/(2sqrt(3) - 1))`

• `tan^-1(sqrt(3)); tan^-1 (sqrt(2)) tan^-1((sqrt(2) + 3)/(3sqrt(2) - 1))`

Answer 1

The angles of a triangle, two of whose sides are represented by the vectors `sqrt(3)(veca xx vecb)` and `vecb - (veca.vecb)veca` where `vecb` is a non-zero vector and `veca` is a unit vector are `underlinebb(tan^-1(sqrt(3)); tan^-1(1/sqrt(3)); cot^-1(0))`.

Explanation:

Let `vecx = sqrt(3)(veca xx vecb)` and `vecy = vecb - (veca.vecb)veca` clearly `vecx.vecy` = 0 `\implies vecx` and `vecy` are perpendicular

So, one angle is `π/2`. Also `|vecx| = sqrt(3)|b sin θ|`, where θ is angle between vectors `veca` and `vecb  (|veca| = 1)`

`|vecy| = sqrt({vecb - (veca.vecb)veca}^2) = sqrt(b^2 - (veca.vecb)^2`

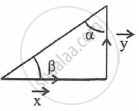
= `sqrt(b^2 - b^2 cos θ) = |b sin θ|`

∴ `|vecx|/|vecy| = sqrt(3)` = tan α `\implies α = π/3`. So, β = `π/6`