Question

The area above the x-axis and under the curve `y = sqrt(1/x - 1)` for `1/2 ≤ x ≤ 1` is:

Options

• `pi/4 - 1/2`

• `pi/4 + 1/2`

• `pi/4 + 1`

• `pi/4 - 1`

Answer 1

`pi/4 - 1/2`

Explanation:

Equation of curve, `y = sqrt(1/x - 1) ⇒ y^2 = 1/x - 1`

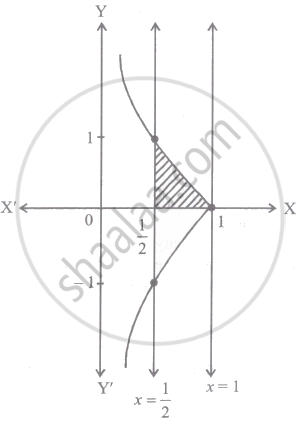
At `x = 1/2 ⇒ y^2 = 2 - 1 ⇒ y = +- 1`

At `x = 1 ⇒ y^2 = 1 - 1 ⇒ y = 0`

Now, the area bounded by x-axis,

`x = 1/2` and `x = 1` is given by, `I = int_(1/2)^1 y  dx`

`I = int_(1/2)^1 sqrt(1/x - 1)  dx`

`I = int_(1/2)^1 sqrt((1 - x)/x)  dx`

Let `x = cos^2 theta`

`dx = 2costheta x - sintheta  d theta`

Limits : `x = 1/2 ⇒ theta = pi/4`

`x = 1 ⇒ theta = 0`

`I = int_(pi/4)^0 sqrt((1 - cos^2 theta)/(cos^2 theta)) x - 2 sin theta cos theta  d theta`

`I = int_(pi/4)^0 sintheta/cos theta x - 2 sin theta cos theta d theta`

`I = int_0^(pi/4) 2sin^2 theta d theta = int_0^(pi/4) (1 - cos 2theta) d theta`

`I = [theta - (sin 2theta)/2]_0^(pi/4)`

`I = [(pi/4 - (sin  pi/2)/2) - (0 - 0)]`

`I = pi/4 - 1/2`

∴ Area, A = `|I| = pi/4 - 1/2` square unit