Question

The area bounded by the curve `y = x|x|`, `x`-axis and the ordinate `x` = – 1 and `x` = 1 is given by

Options

• 0

• `1/3`

• `2/3`

• `4/3`

Answer 1

`2/3`

Explanation:

When `x > 0, |x| = - x`

Equation of the curve is `y = - x^2`

= Area bounded by the curve `y = x|x|`

`x`-axis and ordinates, `x` = – 1, `x` = 1

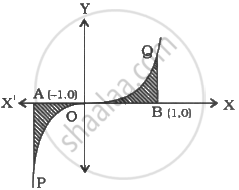
Area of region POA + Area of region ΔBθO = 2 × Area of region ΔBθO

(∵ These areas are equal due to symmetry)

= `2 xx int_0^1 ydx`

= `2xx int_0^1 x^2 dx`

= `2[x^3/3]_0^1`

= `2/3`