Question

The area bounded by the curve `y = x^3`, the `x`-axis and ordinates `x` = – 2 and `x` = 1

Options

• `-9`

• `- 15/4`

• `15/4`

• `17/4`

Answer 1

`17/4`

Explanation:

The curves, `y = x^3`

Differentiate `(dy)/(dx) = 3x^2` = + ve

∴ Curve is an increasing curve `(dy)/(dx) = 0, x = 0`

∴ `x`-axis is the tangent at `x` = 0

`f(-x) = -f(x)` ∴ `(-x)^3 = -x^3`

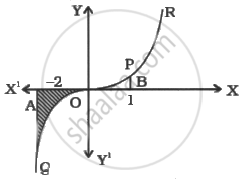
Curve is symmetrical in opposite quadrants.

Area bounded by the curve `y = x^3`, the `x`-axis, `x` = – 2 and `x` = 1.

Area of region AθOBPOA

Area of the region n AθOA + Area of the region ΔBPO

= `|int_(-2)^0 ydx| + int_0^1 ydx = (int_(-2)^0 x^3 dx) + int_0^1 x^3 dx`

= `|[x^4/4]_(-2)^0| + [x^4/4]_0^1`

= `|0 - (-2)^4/4| + (1/4 - 0)`

= `16/4 + 1/4 = 17/4`