Question

The area enclosed by y² = 8x and y = `sqrt(2x)` that lies outside the triangle formed by y = `sqrt(2x)`, x = 1, y = `2sqrt(2)`, is equal to ______.

Options

• `(16sqrt(2))/6`

• `(11sqrt(2))/6`

• `(13sqrt(2))/6`

• `(5sqrt(2))/6`

Answer 1

The area enclosed by y² = 8x and y = `sqrt(2x)` that lies outside the triangle formed by y = `sqrt(2x)`, x = 1, y = `2sqrt(2)`, is equal to `underlinebb((13sqrt(2))/6)`.

Explanation:

Given curves are y² = 8x and y = `sqrt(2)x`

Let us find the intersection point of both the curves:

`(sqrt(2)x)^2` = 8x

⇒ 2x² = 8x

⇒ 2x² – 4x = 0

⇒ x(x – 4) = 0

⇒ x = 0, 4

⇒ y = `0, 4sqrt(2)`

So intersection points are (0, 0) and `(4, 4sqrt(2))`

Let PQR be the triangle formed by y = `sqrt(2)x`, x = 1 and y = `2sqrt(2)`

⇒ P = `(1, 2sqrt(2))`, Q = `(1, sqrt(2))`, R = `(2, 2sqrt(2))`

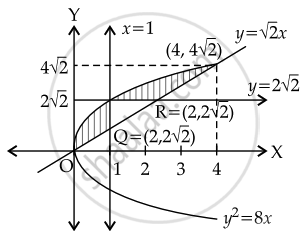
Area of OPSRQ = `int_0^4(sqrt(8x) - sqrt(2x))dx`

= `[sqrt(8)(2/3x^(3/2)) - sqrt(2)/2x^2]_0^4`

= `(2sqrt(8))/3(4)^(3/2) - 1/sqrt(2)(4)^2`

= `(4sqrt(2))/3(8) - 16/sqrt(2)`

⇒ Area of OPSRQ = `((32sqrt(2))/3 - 8sqrt(2))`sq.units

Now, area of ΔPQR = `1/2 xx (PQ) xx (PR)`

= `1/2 xx (2sqrt(2) - sqrt(2)) xx 1`

= `1/2 xx sqrt(2)`

⇒ Area of ΔPQR = `sqrt(2)/2`sq.units

So, Required area = Area of shaded region

= Area of OPSRQ – Area of ΔPQR

= `(32sqrt(2))/3 - 8sqrt(2) - sqrt(2)/2`

= `(64sqrt(2) - 48sqrt(2) - 3sqrt(2))/6`

= `(13sqrt(2))/6`sq.units