Question

The area (in sq. units) of the region {(x, y) : y² ≥ 2x and x² + y² ≤ 4x, x ≥ 0, y ≥ 0} is ______.

Options

• `π - 4/3`

• `π - 8/3`

• `π - (4sqrt(2))/3`

• `π/2 - (2sqrt(2))/3`

Answer 1

The area (in sq. units) of the region {(x, y) : y² ≥ 2x and x² + y² ≤ 4x, x ≥ 0, y ≥ 0} is `underlinebb(π - 8/3)`.

Explanation:

Given, the equation of curve = y² = 2x  ...(i)

Which is a parabola with vertex (0, 0) and its axis parallel to X-axis

and another curve x² + y² = 4x  ...(ii)

Which is a circle with centre (2, 0) and radius is 2.

On substituting y² = 2x in equation (ii), we get

x² + 2x = 4x

`\implies` x² = 2x

`\implies` x(x – 2) = 0

`\implies` x = 0 or x = 2   

`\implies` y = 0 or y = ± 2 ...[Using equation (i)]

Now, the required area is the area of shaded region

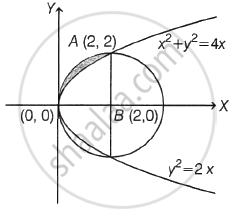
∴ Required area = `"Area of a circle"/4 - int_0^2 sqrt(2x)  dx`

= `(π(2)^2)/4 - sqrt(2) int_0^2 x^(1//2)  dx`

= `π - sqrt(2)[x^(3//2)/(3//2)]_0^2`

= `π - (2sqrt(2))/3 [2sqrt(2) - 0]`

= `(π - 8/3)` sq. units