Question

The area included between the parabolas y² = 4a(x +a) and y² = 4b(x – a), b > a > 0, is

Options

• `(4sqrt(2))/3 b^2 sqrt(a/(b - a)` sq.units

• `(8sqrt(8))/3 a^2 sqrt(b/(b - a)` sq.units

• `(4sqrt(2))/3 a^2 sqrt(b/(b - a)` sq.units

• `(8sqrt(8))/3 b^2 sqrt(a/(b - a)` sq.units

Answer 1

`(8sqrt(8))/3 a^2 sqrt(b/(b - a)` sq.units

Explanation:

We have y² = 4a(x + a) ...(i), a parabola with vertex (– a, 0)

And y² = 4b(x – a) ...(ii), a parabola with vertex (a, 0)

Solving (i) and (ii), we get y = `+-a sqrt((8b)/(b - a)`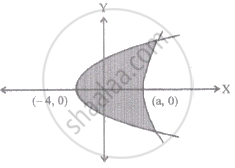

A = `2 int_0^((asqrt(8b))/(sqrt(b - a))) ((y^2/(4b) + a) - (y^2/(4b) - a)) dy`

= `2 int_0^((asqrt(8b))/(sqrt(b - a))) (2a - ((b - a)y^2)/(4ab)) dy`

= `2[2ay - (b - a)/(12ab) y^3]_0^((asqrt(8b))/(sqrt(b - a))`

= `2[2a xx (asqrt(8b))/sqrt(b - a) - (b - a)/(12ab) ((asqrt(8b))/(b - a))^3]`

= `(8a^2)/3 sqrt((8b)/(b - a))` sq.units