Advertisements
Advertisements
Question
The bisector of ∠ B and ∠C of a quadrilateral ABCD intersect in P, show that P is equidistant from the opposite sides AB and CD.
Solution
Given: A quadrilateral ABCD. Bisectors of ∠B and ∠C meet in P. PM ⊥ AB and PN ⊥ CD.
To prove that : PM = PN ...(1)
Construction: Draw PL ⊥ BC
Proof : P lies on bisector or of ∠B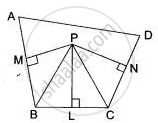
∴ PM = PL
P lies on bisector of ∠C
PL = PN ...(2)
From (1) and (2), we have
PM = PN.
Hence proved.
APPEARS IN
RELATED QUESTIONS
Use ruler and compasses only for the following questions. All constructions lines and arcs must be clearly shown.
Construct the locus of points at a distance of 3.5 cm from A.
Use ruler and compasses only for the following questions. All constructions lines and arcs must be clearly shown
Construct the locus of points equidistant from AC and BC.
Use ruler and compasses only for the following questions. All constructions lines and arcs must be clearly shown
Mark 2 points X and Y which are a distance of 3.5 cm from A and also equidistant from AC and BC. Measure XY.
A point moves such that its distance from a fixed line AB is always the same. What is the relation between AB and the path travelled by the point?
State the locus of a point moving so that its perpendicular distances from two given lines is always equal.
AB is a fixed line) state the locus of the point P such that ∠ APB = 90° .
l is the perpendicular bisector of line segment PQ and R is a point on the same side of l as P. The segment QR intersects l at X. Prove that PX + XR = QR.
Given a Δ ABC with unequal sides. Find a point which is equidistant from B and C as well as from AB and AC.
The diagonals of a quadrilateral bisect each other at right angles. Show that the quadrilateral is a rhombus.
What is the locus of points which are equidistant from the given non-collinear point A, B and C? Justify your answer.
