Question

The centre of mass of a right circular cone of height h, radius R and constant density `sigma` is at ____________.

Options

• `(0,0, "h"/4)`

• `("h"/4/0,0)`

• `("h"/3/0,0)`

• `(0,0, "h"/3)`

Answer 1

The centre of mass of a right circular cone of height h, radius R and constant density `sigma` is at `(0,0, "h"/4)`.

Explanation:

Mass = density x volume

`"dm" = sigma  pi"r"^2 "dz"`

From the figure,

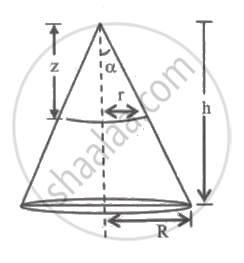`"tan"  alpha = "r"/"z" = "R"/"h"`

`therefore "r" = "R"/"h""z"`

Now,

`"z"_"CM" = (int"zdm")/(int"dM") = (int_0^"h" sigmapi"r"^2  "zdz")/(1/3 pi"R"^2 "h"sigma)`

where, dM = mass element of entire cone.

`therefore "z"_"CM"= 3/("R"^2h) int_0^"h" ("R"/"hz")^2 "zdz"`

`= 3/"hR"^2 ("R"^2/"h"^2) int_0^"h" "z"^3 "dz"`

`= 3/"h"^3 ["z"^4/4]_0^"h"`

`= (3"h")/4`

∴ distance of centre of mass from base is

`"h" - (3"h")/4 = "h"/4`

∴ centre of mass has co-ordinates `(0,0, "h"/4)`