Question

The complex number z = x + iy which satisfy the equation `|(z - 5i)/(z + 5i)|` = 1, lie on ______.

Options

• the X-axis

• the straight line y = 5

• a circle passing through the origin

• None of the above

Answer 1

The complex number z = x + iy which satisfy the equation `|(z - 5i)/(z + 5i)|` = 1, lie on the X-axis.

Explanation:

Given, `|(z - 5i)/(z + 5i)|` = 1

`\implies` |z – 5I| = |z + 5i|

∵ If |z – z₁| = |z – z₂|, then it is a perpendicular bisector of z₁ and z₂.

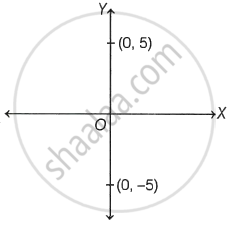
∴ Perpendicular bisector of (0, 5) and (0, – 5) is X-axis.