Question

The coordinates of A, B, C are (6, 3), (–3, 5) and (4, – 2) respectively and P is any point (x, y). Show that the ratio of the areas of triangle PBC and ABC is

Answer 1

We have,

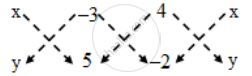
`∴ "Area of ∆PBC" = \frac { 1 }{ 2 } |(5x+6+4y)–(–3y+20–2x)|`

`⇒ "Area of ∆PBC" = \frac { 1 }{ 2 } |5x + 6 + 4y + 3y – 20 + 2x|`

`⇒ "Area of ∆PBC" = \frac { 1 }{ 2 } |7x + 7y – 14|`

`⇒ "Area of ∆PBC" = \frac { 7 }{ 2 } |x + y– 2|`

`⇒ "Area of ∆PBC" = \frac { 7 }{ 2 } |6 + 3 – 2|`

`"[Replacing x by 6 and y = 3 in Area of Delta PBC]"`

`⇒ "Area of ∆ABC" = \frac { 49 }{ 2 }`

`\therefore \frac{Area\ of\ \Delta PBC}{Area\ of\ \Delta ABC}=\frac{\frac{7}{2}|x+y-2|}{\frac{49}{2}}`

`\therefore \frac{Area\ of\ \Delta PBC}{Area\ of\ \Delta ABC}=(x+y-2)/7`