Question

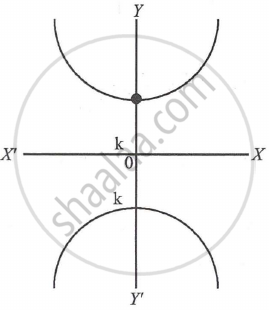
The differential equation of all parabolas whose axis is Y-axis, is ______.

Options

• `x (d^2y)/(dx^2) - dy/dx` = 0

• `x (d^2y)/(dx^2) + dy/dx` = 0

• `(d^2y)/(dx^2) - y` = 0

• `(d^2y)/(dx^2) - dy/dx` = 0

Answer 1

The differential equation of all parabolas whose axis is Y-axis, is `underlinebb(x (d^2y)/(dx^2) - dy/dx = 0)`.

Explanation:

Let vertex of parabola be (0, k) as axis of parabola is Y-axis

So, equation of parabola is

(x – 0)² = 4a (y – k)

`\implies` x² = 4ay – 4ak

After, differentiating both sides w.r.t., 'x', we get

2x = `4a dy/dx`

Therefore, `1/(2a) = 1/x dy/dx`

Again differentiating on both sides w.r.t. 'x', we get

`d/dx(1/x, dy/dx) = d/dx(1/(2a))`

`\implies 1/x.(d^2y)/(dx^2) + dy/dx(-1/x^2)` = 0

Hence, `x (d^2y)/(dx^2) - dy/dx` = 0