Question

The distance of the origin from the centroid of the triangle whose two sides have the equations. x – 2y + 1 = 0 and 2x – y – 1 = 0 and whose orthocenter is `(7/3. 7/3)` is ______.

Options

• `sqrt(2)`

• 2

• `2sqrt(2)`

• 4

Answer 1

The distance of the origin from the centroid of the triangle whose two sides have the equations. x – 2y + 1 = 0 and 2x – y – 1 = 0 and whose orthocenter is `(7/3, 7/3)` is `underline(2sqrt(2))`.

Explanation:

Given: Coordinates of ortho of triangle is H =  `(7/3, 7/3)`

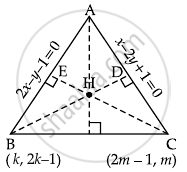
Let equation of line AB: 2x – y – 1 = 0 ...(i)

And equation of line AC: x – 2y + 1 = 0 ...(ii)

On solving equation (i) and equation (ii), we get x = 1, y = 1

∴ Coordinates of point A is (1, 1)

Let coordinates of point B be (k, 2k – 1) and C be (2m – 1, m)

Now, slope of AC × slope of BD = –1

⇒ `(1/2)((7/3 - 2k + 1)/(7/3 - k))` = –1

⇒ k = 2

Now, slope of AB × slope of CE = –1

⇒ (2) = `((7/3 - m)/(7/3 - 2m + 1))` = –1

⇒ m = 2

∴ A(1, 1), B(2, 3), C(3, 2)

Now, coordinates of centroid

G = `((1 + 2 + 3)/3, (1 + 3 + 2)/3)` = (2, 2)

∴ OG = `sqrt(2^2 + 2^2) = 2sqrt(2)`