Advertisements
Advertisements
Question
The distance of the point P(2, 3) from the x-axis is ______.
Options
2
3
1
5
Solution
The distance of the point P(2, 3) from the x-axis is 3.
Explanation:
We know that,
(x, y) is a point on the cartesian plane in first quadrant.
Then,
x = Perpendicular distance from Y-axis and
y = Perpendicular distance from X-axis
Therefore, the perpendicular distance from X-axis = y coordinate = 3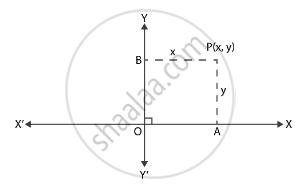
APPEARS IN
RELATED QUESTIONS
Find the value of x such that PQ = QR where the coordinates of P, Q and R are (6, -1), (1, 3) and (x, 8) respectively.
Name the quadrilateral formed, if any, by the following points, and given reasons for your answers:
A(-1,-2) B(1, 0), C (-1, 2), D(-3, 0)
In the seating arrangement of desks in a classroom three students Rohini, Sandhya and Bina are seated at A(3, 1), B(6, 4), and C(8, 6). Do you think they are seated in a line?
Find the points of trisection of the line segment joining the points:
(3, -2) and (-3, -4)
In what ratio is the line segment joining (-3, -1) and (-8, -9) divided at the point (-5, -21/5)?
The line segment joining the points A(3,−4) and B(1,2) is trisected at the points P(p,−2) and Q `(5/3,q)`. Find the values of p and q.
If the point `P (1/2,y)` lies on the line segment joining the points A(3, -5) and B(-7, 9) then find the ratio in which P divides AB. Also, find the value of y.
The measure of the angle between the coordinate axes is
If P ( 9a -2 , - b) divides the line segment joining A (3a + 1 , - 3 ) and B (8a, 5) in the ratio 3 : 1 , find the values of a and b .
If the vertices of a triangle are (1, −3), (4, p) and (−9, 7) and its area is 15 sq. units, find the value(s) of p.
What is the area of the triangle formed by the points O (0, 0), A (6, 0) and B (0, 4)?
If P (x, 6) is the mid-point of the line segment joining A (6, 5) and B (4, y), find y.
If points (a, 0), (0, b) and (1, 1) are collinear, then \[\frac{1}{a} + \frac{1}{b} =\]
The ratio in which the line segment joining points A (a1, b1) and B (a2, b2) is divided by y-axis is
In which quadrant does the point (-4, -3) lie?
Assertion (A): The ratio in which the line segment joining (2, -3) and (5, 6) internally divided by x-axis is 1:2.
Reason (R): as formula for the internal division is `((mx_2 + nx_1)/(m + n) , (my_2 + ny_1)/(m + n))`
Statement A (Assertion): If the coordinates of the mid-points of the sides AB and AC of ∆ABC are D(3, 5) and E(–3, –3) respectively, then BC = 20 units.
Statement R (Reason): The line joining the mid-points of two sides of a triangle is parallel to the third side and equal to half of it.
Distance of the point (6, 5) from the y-axis is ______.
Assertion (A): Mid-point of a line segment divides the line segment in the ratio 1 : 1
Reason (R): The ratio in which the point (−3, k) divides the line segment joining the points (− 5, 4) and (− 2, 3) is 1 : 2.
