Question

The equation of the parabola whose vertex and focus are on the positive side of the x-axis at distances a and b respectively from the origin is ______.

Options

• y² = 4(b – a)(x – a)

• y² = 4(a – b)(x – b)

• x² = 4(b – a)(y – a)

• x² = 4(a – b)(y – b)

Answer 1

The equation of the parabola whose vertex and focus are on the positive side of the x-axis at distances a and b respectively from the origin is `underlinebb(y^2 = 4(b - a)(x - a))`.

Explanation:

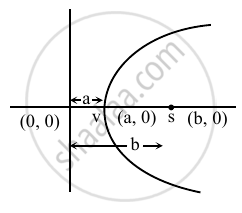
Let equation of parabola is (y – y₁)² = 4A(x – x₁)

Here A = (b – a)

and vertex = (x₁, y₁) ≡ (a, 0)

∴ Equation will be (y – 0)² = 4(b – a)(x – a)

⇒ y² = 4(b – a)(x – a)